Explanation
Units of measurements
In the explanation below we simply use the term ‘units’ to describe all types of measurements.
For the simulation we used special units that simplify the visualization. See details below.
Potential vs. Kinetic Energy
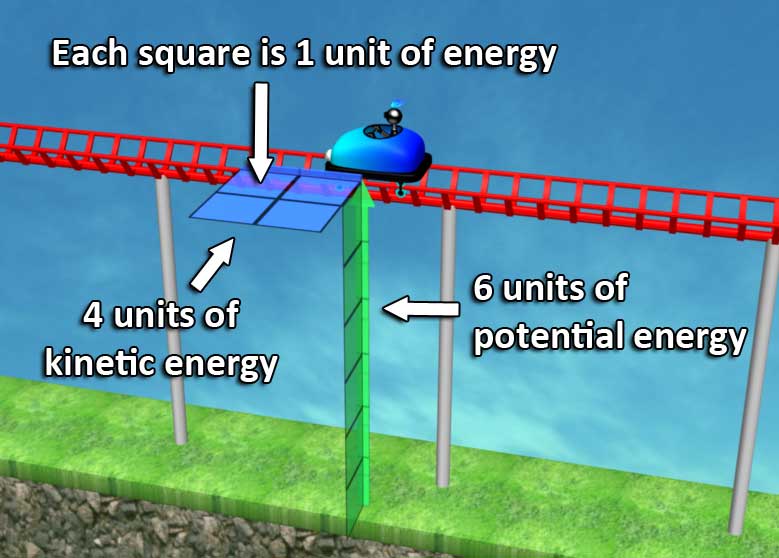
At the start of the video we see a cart travelling at a height of 6 units above ground, and velocity of 2 units. Potential energy is proportional to the cart’s mass (which is constant), and to the height. Kinetic energy is proportional to the mass and to the velocity squared.
So each square represents one unit of energy. We start with 6 units of potential energy, and 4 units of kinetic energy.
The first 40 seconds of the video show how these 10 units of energy shift from potential to kinetic energy, as the cart is travelling up and down.
In real life of course some kinetic energy is converted to heat due to friction, and the cart gradually slows down.
Elastic Collision #1
An elastic collision is a collision where all the kinetic energy remains kinetic energy. An example of an almost purely elastic collision is two billiard balls colliding, and transferring their kinetic energy from one to the other. A non-elastic collision, called plastic collision, is for example when car keys hit the ground. Their kinetic energy is converted to heat, and they stop moving.
The first collision shown in the video is simple: all 4 units of kinetic energy pass from the blue cart to the green cart.
Cliff drop

Elastic Collisions #2 and #3

The first collision is simple: both carts have the same mass.
In the second collision we introduce a double cart. Since energy is also proportional to mass, this cart has double amount of potential energy for the same height, and double amount of kinetic energy for the same velocity. In the video we chose to visualize this using double plates of units.
To calculate what happens in this collision we need to take into account also the law of conservation of momentum. Momentum is the mass multiplied by velocity.
So before the collision we have:

And after the collision:

As you can see, the total of 9 units of kinetic energy and 3 units of momentum are conserved.
If all the kinetic energy would have moved to the double cart, the double cart would have had a velocity of 2.12, and momentum of 4.24, violating conservation of momentum.
In the third collision we have:
Total kinetic energy: 18 units.
Total momentum: 6 units.
The spring

As a spring is compressed it gathers what is called elastic energy. The elastic energy of a spring is proportional to the square of the distance it is displaced.
So we can see the cart losing kinetic energy in favor of elastic energy, and then the spring starts to push it backwards, giving all the energy back.
Units of measurements

Here are some technical details about the units of measurements we used.
Distance: the energy squares in the video are 1 meter in length. You might think that for an animated video the scale is not really relevant, but it is. We simulated the usual earth acceleration of 9.8 m /sec ^2, so it’s important to set the scale.
Time: instead of measuring time in seconds, we measure it in units we call nifty-seconds. One nifty-second is 0.22576 second. This is important for the velocity measurements. 2 units of velocity, as shown for example in the picture on the left, means 2 meters per nifty-second. That’s 8.859 meters per second, 31.9 km/h, or 19.8 mph.
The reason we chose to use nifty-seconds is that the earth’s acceleration (9.8 meters per second^2) in nifty-seconds is 0.5 meters per nifty-second^2. The full formulas of kinetic and potential energy are:
Kinetic energy: m v^2 /2
Potential energy: mgh
Substituting g (earth’s acceleration) with 0.5, and m=2, we get that the kinetic energy is v^2 and the potential energy is h. This allows us to draw a rectangle representing a unit of energy per unit of velocity squared and per meter of height on the same scale. Now that’s nifty.
If we assume the mass of the cart is 10 kilograms (22.05 pounds), then a single energy square is 98 joule or 23.42 calories. The simulation in the video doesn’t need to assume any particular mass to the cart.
